스마트 컨트랙트에서의 Merkle Proof 사용
Introduction
NFT 프로젝트에서 화이트 리스트 명단만 NFT 민팅이 가능하게 만드는 시나리오처럼, 특정한 주소 리스트들만 함수를 실행할 수 있도록 스마트 컨트렉트를 작성하려면 어떻게 해야할까? 이더리움의 저장 공간과 비용에 제약이 없다면 모든 주소 리스트들을 Storage에 매핑 형태로 저장한 후, 트랜잭션 요청 시 msg.sender가 매핑 값을 갖는지 확인하는 것이 하나의 방법일 것이다. 하지만 이더리움 네트워크는 수 많은 컴퓨터가 상태를 공유하는 월드 컴퓨터로서, 이러한 월드 컴퓨터에 데이터를 저장하는 것은 많은 비용이 소모된다 (32 bytes의 word를 저장하는 것은 통상적으로 20,000 gas를 소모, 글쓴 시점 기준 약 8천원).
이러한 공간과 비용의 문제를 해결하기 위해, 스마트 컨트렉트에서는 Merkle Proof라는 방식을 사용한다. Merkle Proof를 이용하면 모든 주소 데이터를 Storage에 저장하지 않고도, 특정 주소 데이터가 함수 실행 허용 주소 목록에 들어가는지 아닌지를 판단할 수 있다. 즉 모든 데이터 (여기선 주소 리스트)를 이더리움 온체인에 저장하지 않고도 아주 작은 온체인 데이터만으로도 (뒤에 나올 Merkle Tree의 Root 값), 특정 데이터의 무결성(Data integrity)을 검증할 수 있다.
Merkle Proof and Merkle Tree
Merkle Proof는 머클 트리(Merkle Tree)를 사용한다. 아래 그림과 같이 머클 트리의 Leaf 노드는 데이터의 해시 값으로 구성되어 있으며, Leaf 노드가 아닌 모든 노드들은 자식 노드 둘의 해시 값을 가진다. Leaf 노드의 데이터 값이 하나라도 변경된다면, 해시 함수의 결과 값이 계층마다 연쇄적으로 달라지기 때문에 Root node의 해시 값이 완전히 달라지게 된다. 우리는 이 Root Hash 값만을 이더리움 온체인에 저장함으로써 특정 데이터가 해당 머클 트리에 포함되어 있는지를 검증할 수 있다. 예시를 들어 보자.
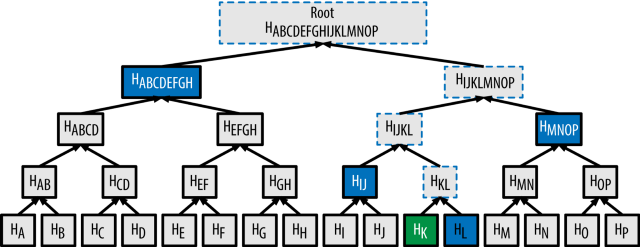
위 그림에서 Leaf 노드 H(K)가 해당 머클 트리에 포함된다는 것을 스마트 컨트렉트에서 어떻게 증명할 수 있을까? 여기서 해당 머클 트리의 Root Hash 값 H(ABCDEFGHIJKLMNOP)은 온체인에 저장되어 퍼블릭하게 공개되어 있다고 가정해보자. 우리는 위 그림에서 색칠된 노드들만 있다면 해시 계산을 통해 Root Hash 값을 도출할 수 있다. 계산은 다음과 같다.
- H(K)을 H(L)와 해싱하여 H(KL)을 계산
- H(KL)을 H(IJ)와 해싱하여 H(IJKL)을 계산
- H(IJKL)을 H(MNOP)와 해싱하여 H(IJKLMNOP)을 계산
- H(IJKLMNOP)을 H(ABCDEFGH)와 해싱하여 Root Hash인 H(ABCDEFGHIJKLMNOP)을 계산
따라서 H(K)로부터 Root Hash 값을 구하기 위해선 [ H(K), H(L), H(IJ), H(MNOP), H(ABCDEFGH)] 값들이 필요하다. 위 과정을 통해 계산된 Root Hash 값이 미리 온체인에 저장되어 있던 Root Hash 값과 일치한다면 우리는 Leaf H(K)가 H(ABCDEFGHIJKLMNOP)를 Root Hash로 가지는 머클 트리에 포함되었다고 판단할 수 있다.
Warning: 위 해시함수 계산 과정에선 해시함수 파라미터들의 순서(order)를 무시하였지만, H(H(KL), H(IJ))의 값은 H(H(IJ), H(KL))) 값과 전혀 다를 수 있기 때문에 실제 구현에선 파라미터의 순서 혹은 Concat 순서에 유의해야한다. 아래 살펴볼 OpenZeppelin 라이브러리에서는 H(IJ)와 H(KL)의 값의 크기를 비교하여 정렬한다. 즉 H(IJ)가 H(KL)보다 클 때, H(concat(H(IJ),H(KL)))을 수행하고, 반대의 경우엔 H(concat(H(KL),H(IJ)))를 수행한다.
위의 예제처럼 특정 데이터(A to P)들의 집합이 있을 때, 우리는 이 데이터들의 해시 값을 Leaf 노드로 하여 머클 트리를 구성할 수 있다. 이 때 Merkle Proof는 특정 데이터가 해당 머클 트리에 속해있는지를 검증하는 방법이다. 스마트 컨트렉트 스토리지에 머클 트리의 Root Hash 값을 미리 저장하고, 추후 사용자가 특정 데이터가 해당 머클 트리에 속해있는지 증명하기 위해 Proof를 전달할 수 있다. 여기서 Proof는 모든 데이터를 포함 할 필요 없이, Root Hash를 재구성하기 위한 최소한의 값들만을 포함하면 된다 (앞선 예시에서 Proof는 모든 데이터 A,…,P 가 아닌 H(K), H(L), H(IJ), H(MNOP), H(ABCDEFGH)만 필요하였다).
OpenZeppelin의 Merkle Proof 라이브러리
오픈제플린(OpenZeppelin)에서는 Merkle Proof를 안전하고, 쉽게 구현할 수 있도록 라이브러리를 제공하고 있다. Merkle Tree와 Proof를 생성하기 위한 Javascript 라이브러리와, 이를 온체인상에서 검증하기 위한 Merkle Proof 솔리디티 라이브러리가 별개로 존재한다.
오픈제플린의 라이브러리에선 이더리움 스마트 컨트렉트를 위한 “표준” 머클 트리(Standard Merkle Trees)를 사용한다. 스탠다드 머클 트리의 특징은 다음과 같다.
- 완전 이진 트리이다
- Leaves는 크기가 큰 순부터 작은 순으로 정렬되어 있다
- Leaves는 일련의 값을 ABI encoding한 결과이다
- Keccak256 해시함수를 사용한다
- Second preimage attacks를 방지하기 위해 Leaves는 데이터를 두번 해싱한 값을 사용한다
위 사항들 중 아래 3가지 사항을 고려할 때 Leaf는 솔리디티에서 아래와 같이 표현된다.
bytes32 leaf = keccak256(bytes.concat(keccak256(abi.encode(addr, amount))));
그럼 이제 자바스크립트 라이브러리를 통해 스탠다드 트리를 구성해보자. “npm install @openzeppelin/merkle-tree” 명령어를 통해 패키지를 설치할 수 있다. 우리는 자바스크립트 라이브러리를 통해 필요한 데이터로부터 Merkle Tree를 생성하고, 특정 데이터의 Proof를 출력할 수 있다. 또한 Tree를 Json 파일로 저장하여, 퍼블릭에 공개해 누구나 tree를 재구성하고, proof를 생성하도록 만들 수 있다. 아래 예제를 살펴보자.
import { StandardMerkleTree } from "@openzeppelin/merkle-tree";
import fs from "fs";
// (1) Data
const values = [
["0x1111111111111111111111111111111111111111", "3000000000000000000"],
["0x2222222222222222222222222222222222222222", "0"],
["0x3333333333333333333333333333333333333333", "30"],
["0x4444444444444444444444444444444444444444", "1500000000000000000"],
];
// (2) 데이터로부터 StandardMerkleTree 생성
const tree = StandardMerkleTree.of(values, ["address", "uint256"]);
// (3) 생성한 standard merkle tree 출력
console.log("Tree:\n" + tree.render());
// (4) 생성한 머클 트리를 json file로 저장
fs.writeFileSync("tree.json", JSON.stringify(tree.dump()));
// (5) json 파일로 저장된 머클 트리를 불러오기
const tree_load = StandardMerkleTree.load(JSON.parse(fs.readFileSync("tree.json")));
// (6) 내가 원하는 데이터의 index를 찾기 위해 entries() 함수를 통한 Loop문 실행
for (const [i, v] of tree_load.entries()) {
if (v[0] === '0x1111111111111111111111111111111111111111') {
// (7) entry의 index를 사용해 원하는 데이터의 proof를 생성
const proof = tree_load.getProof(i);
console.log('Value:', v);
console.log('Proof:', proof);
}
}
위 코드에서, 우리는 하나의 데이터를 [“address”, “uint256”] 값으로 구성하였다. (2)번 StandardMerkleTree를 생성하는 과정에서 이러한 데이터 Type을 알려줌으로써 라이브러리가 Solidity ABI.encode에 맞춰 데이터를 인코딩 할 수 있게한다.
(3)번에서 tree.render() 함수를 통해 콘솔에 출력한 머클 트리의 값은 아래와 같다. 3, 4, 5, 6번 노드는 Leaf 노드로서, 앞서 말한 Standard Merkle Tree의 특징으로 말했 듯 Data를 그대로 사용하지 않고 데이터에 대해 Kecca256 해시함수를 두번 실행한 값이다. 여기서 0번 노드인 “b56f9de6e47f3f111e77cca1c44d90b31d4e140910a68734860a5c3da76a4b27” 값은 Root Hash 값으로서 컨트렉트에 공개적으로 저장되어야할 값이다.
Tree:
0) b56f9de6e47f3f111e77cca1c44d90b31d4e140910a68734860a5c3da76a4b27
├─ 1) 5cad1d68954860301ed48598eea08649201682d2b50c9977d697cb153e0d3618
│ ├─ 3) fdb74f493e905caded8ad7315cf41616f81342fd1fcaf89145801702c4239c2f
│ └─ 4) 81722ecd3bc2b003be5b8850a4de98dc3e991dd001e8173e408de279c388bc2e
└─ 2) b77c1086d6ac2a0e454607cbe31c25dd5736f1bf9c147a6de93cc7121b7d210b
├─ 5) 43ab72a115a26a347338741504964163dea922ee399341883ba5705ea9a4f7d6
└─ 6) 4358fbda895975ea76fcee263adef8867647f91879de2c1a3c257821709287a5
여기서 Leaf 노드의 순서는 데이터의 입력 순서(Values 배열의 인덱스 순서)가 아니라는 점을 명심해야한다. Leaf 노드는 앞서 말했 듯, 크기에 따라 ‘정렬’된다. 첫번째 Leaf 노드 “fdb74f493e905caded8ad7315cf41616f81342fd1fcaf89145801702c4239c2f”가 가장 큰 값을 가짐을 확인할 수 있으며 이 값은 Values[0]인 [“0x1111111111111111111111111111111111111111”, “3000000000000000000”]을 두번 해싱한 값이 아닌, Values[3]을 두번 해싱한 값이다. 아래 코드를 통해 우리는 이를 확인할 수 있다.
const leaf = tree.leafHash(values[3]);
console.log("Leaf of values[3]: " + leaf);
Leaf of values[3]: 0xfdb74f493e905caded8ad7315cf41616f81342fd1fcaf89145801702c4239c2f
즉, 오픈제플린에서 사용하는 표준 머클 트리에선 데이터들에 대해 Kecca256 해시 함수를 실행하여 해시 값을 먼저 구한 후, 크기가 큰 순으로 정렬하여 Leaf 노드로 삼는다.
다시 본래 코드로 돌아와 (6)번 과정을 살펴보자.
// (6) 내가 원하는 데이터의 index를 찾기 위해 entries() 함수를 통한 Loop문 실행
for (const [i, v] of tree_load.entries()) {
if (v[0] === '0x1111111111111111111111111111111111111111') {
// (7) entry의 index를 사용해 원하는 데이터의 proof를 생성
const proof = tree_load.getProof(i);
console.log('Value:', v);
console.log('Proof:', proof);
}
}
우리는 생성한 머클 트리에서 특정 데이터를 위한 Proof를 생성할 수 있다. 예제에선, “0x1111111111111111111111111111111111111111”의 주소를 가진 데이터를 위해 Proof를 생성한다. Proof를 출력한 결과는 다음과 같다.
Proof: [
'0x4358fbda895975ea76fcee263adef8867647f91879de2c1a3c257821709287a5',
'0x5cad1d68954860301ed48598eea08649201682d2b50c9977d697cb153e0d3618'
]
우리는 이 Proof를 “0x1111111111111111111111111111111111111111”의 Leaf 해시 값과 함께 스마트 컨트렉트에 보내면 컨트렉트는 이를 통해 Root hash 값을 도출할 수 있다. 도출된 값이 컨트렉트에 스토리지에 사전에 저장된 Root Hash 값인 “b56f9de6e47f3f111e77cca1c44d90b31d4e140910a68734860a5c3da76a4b27”과 동일하다면, 스마트 컨트렉트는 이 데이터가 해당 머클 트리에 속해있는 데이터라고 판단할 수 있다.
그럼 위 과정을 스마트 컨트렉트에서 실제로 어떻게 구현했는지 오픈제플린의 컨트렉트 라이브러리를 살펴보자.
library MerkleProof {
/**
* @dev Returns true if a `leaf` can be proved to be a part of a Merkle tree
* defined by `root`. For this, a `proof` must be provided, containing
* sibling hashes on the branch from the leaf to the root of the tree. Each
* pair of leaves and each pair of pre-images are assumed to be sorted.
*/
function verify(
bytes32[] memory proof,
bytes32 root,
bytes32 leaf
) internal pure returns (bool) {
return processProof(proof, leaf) == root;
}
/**
* @dev Returns the rebuilt hash obtained by traversing a Merkle tree up
* from `leaf` using `proof`. A `proof` is valid if and only if the rebuilt
* hash matches the root of the tree. When processing the proof, the pairs
* of leafs & pre-images are assumed to be sorted.
*
* _Available since v4.4._
*/
function processProof(bytes32[] memory proof, bytes32 leaf) internal pure returns (bytes32) {
bytes32 computedHash = leaf;
for (uint256 i = 0; i < proof.length; i++) {
computedHash = _hashPair(computedHash, proof[i]);
}
return computedHash;
}
function _hashPair(bytes32 a, bytes32 b) private pure returns (bytes32) {
return a < b ? _efficientHash(a, b) : _efficientHash(b, a);
}
function _efficientHash(bytes32 a, bytes32 b) private pure returns (bytes32 value) {
/// @solidity memory-safe-assembly
assembly {
mstore(0x00, a)
mstore(0x20, b)
value := keccak256(0x00, 0x40)
}
}
위 코드는 본래 라이브러리에서 verify와 관련된 함수만을 보여준다. verify는 우리가 앞서 자바스크립트 라이브러리에서 구했던 Proof 값, Merkle Tree의 Root Hash 값, Leaf 값을 전달받으며, Leaf와 Proof를 통해 재계산된 Root Hash 값이 파라미터로 전달된 root 변수와 일치하는지를 판단한다.
라이브러리를 사용하는 입장에서 세부 구현까지 알 필요는 없지만, _hashPair 함수를 살펴보자. 앞서 Warning 구문에서 언급했듯이, Hash(A,B)와 Hash(B,A)는 큰 차이를 가진다. _hashPair 함수에선 A, B의 중 큰 값을 가진 bytes32 값을 첫번째 파라미터로 삼는다. 컨트렉트에서는 이러한 기준을 통해 두개의 자식 노드로부터 부모 노드의 해시 값을 계산할 때 순서에 대해 고민할 필요가 없다.
마지막으로 _efficientHash 함수에서는 실제로 해시 함수가 실행되는 부분이며 자바스크립트와 마찬가지로 Keccak256 해시함수를 사용한다. 여기서는 가스 비용을 절약하기 위해 assembly를 사용하였다. assembly의 동작 과정은 다음과 같다.
- mstore(0x00, a)는 bytes32 a 값을 0x00 메모리 위치에 저장한다.
- mstore(0x20, b)는 bytes32 b 값을 0x20 (10 진수로 32) 메모리 위치에 저장한다.
- keccak256(0x00, 0x40)는 메모리 0x00부터 0x40 (10 진수로 64) 길이만큼의 메모리를 해싱한다.
NFT 프로젝트에서의 실제 활용
앞서 Intro에서 간단히 말했 듯, 많은 NFT 프로젝트에서 White list (WL) 민팅을 진행하고자 할 때 머클 트리를 사용한다. 모든 WL 주소를 온체인에 저장할 필요 없이, 주소 데이터로 구성된 머클 트리의 Root Hash 값만 온체인에 저장하면 되기 때문이다. 아래는 오픈제플린의 라이브러리를 활용하는 테스트 컨트렉트이다. Mint 함수를 실행하고자 하는 트랜잭션의 msg.sender가 머클 트리에 포함되어 있는지를 검증한다. 단순함을 위해 최대한 간결하게 작성되었다.
// SPDX-License-Identifier: GPL-3.0
pragma solidity ^0.8.10;
import "@openzeppelin/contracts/utils/cryptography/MerkleProof.sol";
import "@openzeppelin/contracts/token/ERC721/ERC721.sol";
contract MerkleTest is ERC721 {
/// @notice Merkle root of mint mintlist.
bytes32 public immutable merkleRoot;
/// @notice Id of the most recently minted.
uint256 public id;
/// @notice Mapping to keep track of which addresses have claimed from mintlist.
mapping(address => bool) public hasClaimedMintlist;
error AlreadyClaimed();
error InvalidProof();
/// @param _merkleRoot Merkle root of mint mintlist.
constructor(bytes32 _merkleRoot) ERC721("Your NFT", "TEST"){
merkleRoot = _merkleRoot;
}
/// limit is enforced during the creation of the merkle proof, which will be shared publicly.
/// @param proof Merkle proof to verify the sender is mintlisted.
/// @return nftId The id of the gobbler that was claimed.
function allowlistMint(bytes32[] calldata proof) external returns (uint256 nftId) {
// If the user has already claimed, revert.
if (hasClaimedMintlist[msg.sender]) revert AlreadyClaimed();
// Calculate leaf from msg.sender value
bytes32 leaf = keccak256(bytes.concat(keccak256(abi.encode(msg.sender))));
// If the user's proof is invalid, revert.
if (!MerkleProof.verify(proof, merkleRoot, leaf)) revert InvalidProof();
hasClaimedMintlist[msg.sender] = true;
_mint(msg.sender, id++);
return id;
}
}
위 코드를 살펴보면, 생성자 (constructor) 함수에서 Merkle Tree의 Root Hash 값을 입력받고 있으며, 이는 merkleRoot 변수에 저장된다. 이는 WL 주소 데이터들을 기반으로 생성한 머클 트리의 Root Hash 값을 컨트렉트 Deploy 시점에 입력해야 한다는 것을 의미하며, 특정 주소가 proof 값과 함께 mint를 요청할 때 재계산된 Root Hash 값을 merkleRoot 변수와 비교한다. 재계산된 해시 값이 merkleRoot 변수와 일치할 경우 우리는 해당 주소가 WL 주소 목록에 포함된다는 것을 확인할 수 있다. 이러한 과정이 allowlistMint 함수에 담겨있다.
allowlistMint 함수에선 msg.sender 값을 기반으로 Leaf를 계산한다. 여기선 standard merkle tree의 기준에 따라 Keccak256 해시함수를 두번 사용하였으며, ABI encoding을 사용한다. if (!MerkleProof.verify(proof, merkleRoot, leaf))에서는 유저가 제출한 proof와 유저의 주소로 계산된 leaf를 통해 머클 트리의 Root hash 값을 계산하며, 이를 merkleRoot 값과 비교한다. 일치하지 않는다면, if 문이 참이되므로 error가 발생한다. 만약 일치한다면, hasClaimedMintlist[msg.sender] = true;를 통해 해당 주소가 민팅을 수행했음을 기록하여 추후 다시 민팅을 하지 못하도록 한다. 마지막으로 ERC721로부터 상속받은 함수인 _mint(msg.sender, id++);를 통해 실제 NFT 민팅을 수행한다.
이제 Remix IDE를 통해 위의 코드를 실제로 테스트해보자. 해당 코드를 테스트하기에 앞서 우리는 WL 주소 목록들의 Merkle Tree를 미리 생성해 Root Hash 값을 구해야한다. 이를 위해 아래 자바스크립트 코드에선 주소 4개로 구성된 머클 트리를 생성하였다. 또한, Remix IDE에서 테스트할 주소인 “0x5B38Da6a701c568545dCfcB03FcB875f56beddC4” 주소에 대한 Proof를 생성한다.
import { StandardMerkleTree } from "@openzeppelin/merkle-tree";
const allowlist = [
["0x5B38Da6a701c568545dCfcB03FcB875f56beddC4"],
["0xAb8483F64d9C6d1EcF9b849Ae677dD3315835cb2"],
["0x4B20993Bc481177ec7E8f571ceCaE8A9e22C02db"],
["0x78731D3Ca6b7E34aC0F824c42a7cC18A495cabaB"],
];
const tree = StandardMerkleTree.of(allowlist, ["address"]);
console.log('Merkle Root:', tree.root);
for (const [i, v] of tree.entries()) {
if (v[0] === '0x5B38Da6a701c568545dCfcB03FcB875f56beddC4') {
const proof = tree.getProof(i);
console.log('Address:', v);
console.log('Proof:', proof);
}
}
위 자바스크립트의 실행 결과는 다음과 같다. 우리는 Merkle Root의 값 “0x392dd2679d5481c8d088bcb22272b2054d3939e240c64da9834995e924192bcd”을 컨트렉트 Deploy 시점에 입력해야하며, Proof 값을 allowlistMint 함수 호출 시점에 입력해야한다.
Merkle Root: 0x392dd2679d5481c8d088bcb22272b2054d3939e240c64da9834995e924192bcd
Address: [ '0x5B38Da6a701c568545dCfcB03FcB875f56beddC4' ]
Proof: [
'0x56380595800b450765bcee141fd0b9ded9d8bfc454bd205dd31154e2d4bd104f',
'0xb4422d6cb3cccffbfad08f58e6c0c8fdc1bcbbe3d198eafb4175d29290b5854f'
]
[Finished in 1.037s]
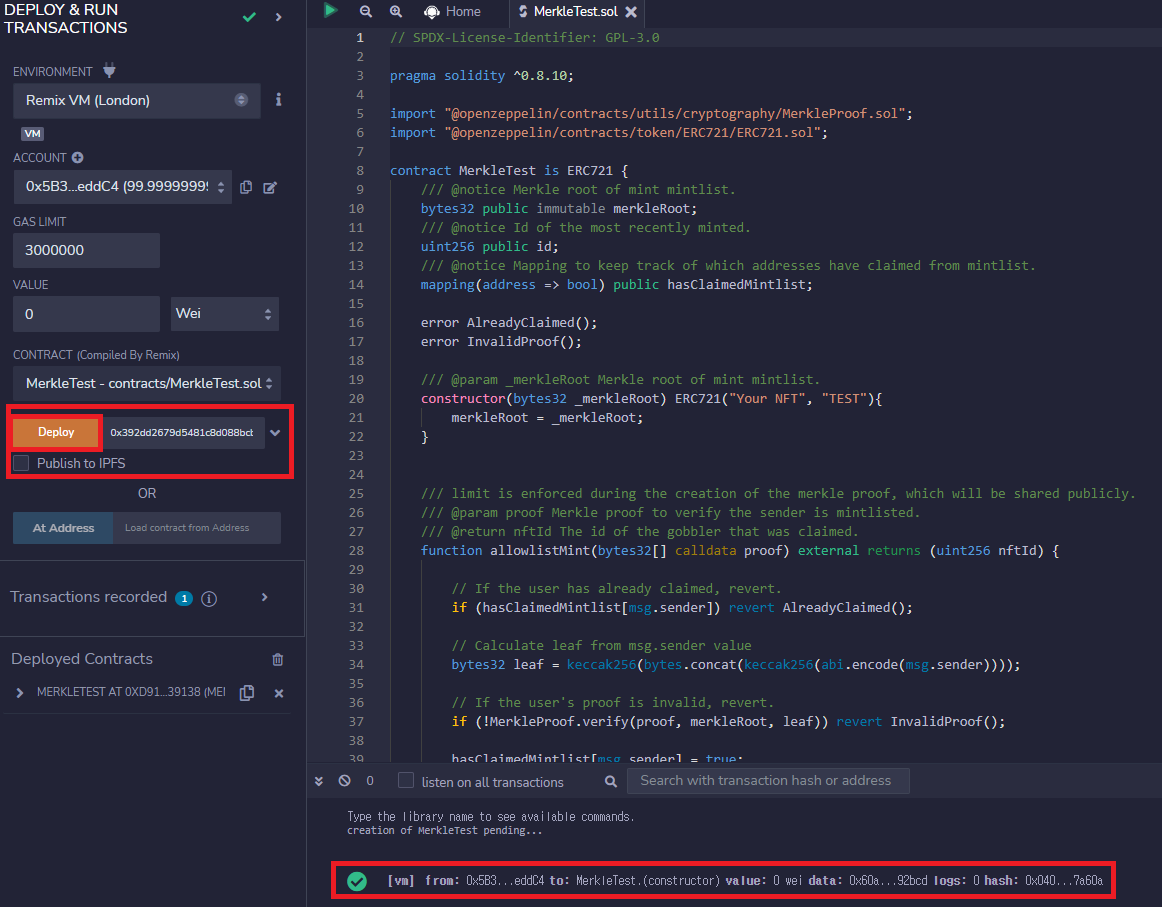
그럼 이제 Remix IDE를 통해 위의 솔리디티 코드를 배포해보자. Deploy의 인자로 위에서 구한 머클 트리의 Root Hash 값인 0x392dd2679d5481c8d088bcb22272b2054d3939e240c64da9834995e924192bcd를 입력해주자. Deploy를 누르면 성공적으로 배포되었다는 메시지를 볼 수 있다.
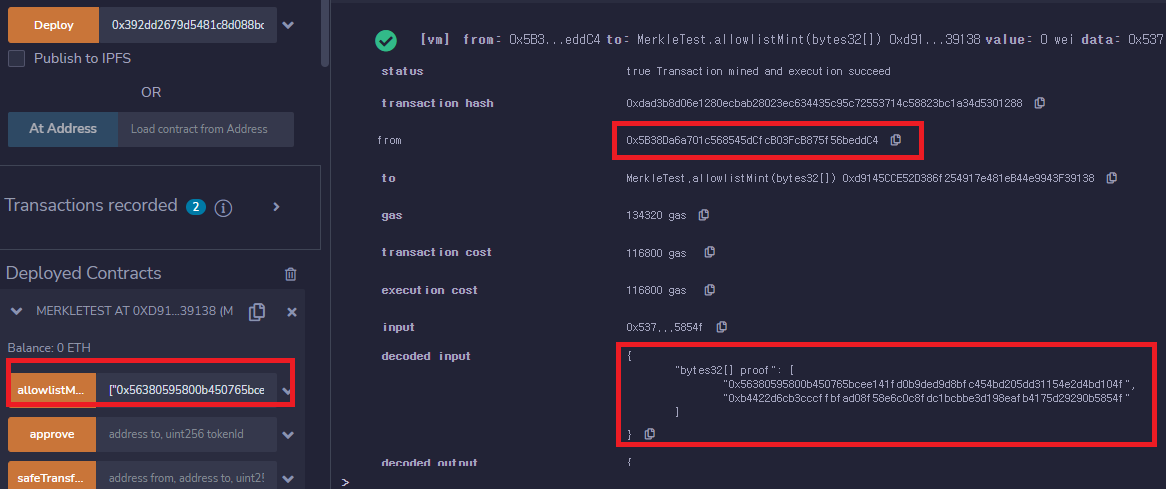
그럼 이제 mint를 진행해보자. allowlistMint 함수의 파라미터로 proof인 ["0x56380595800b450765bcee141fd0b9ded9d8bfc454bd205dd31154e2d4bd104f", "0xb4422d6cb3cccffbfad08f58e6c0c8fdc1bcbbe3d198eafb4175d29290b5854f"]을 파라미터로 allowlistMint 버튼을 클릭한다. from이 0x5B38Da6a701c568545dCfcB03FcB875f56beddC4이 머클 트리에 속해있으므로 성공적으로 민팅이 수행됐음을 알 수 있다. 다만 트랜잭션을 실행한 주소가 0x5B38Da6a701c568545dCfcB03FcB875f56beddC4이 아니라면 트랜잭션은 실패할 것이다. remix에서 사용할 수 있는 0x5B38Da6a701c568545dCfcB03FcB875f56beddC4 주소는 어느 PC 환경에서도 똑같이 사용할 수 있으므로 이를 테스트 해볼 수 있을 것이다.
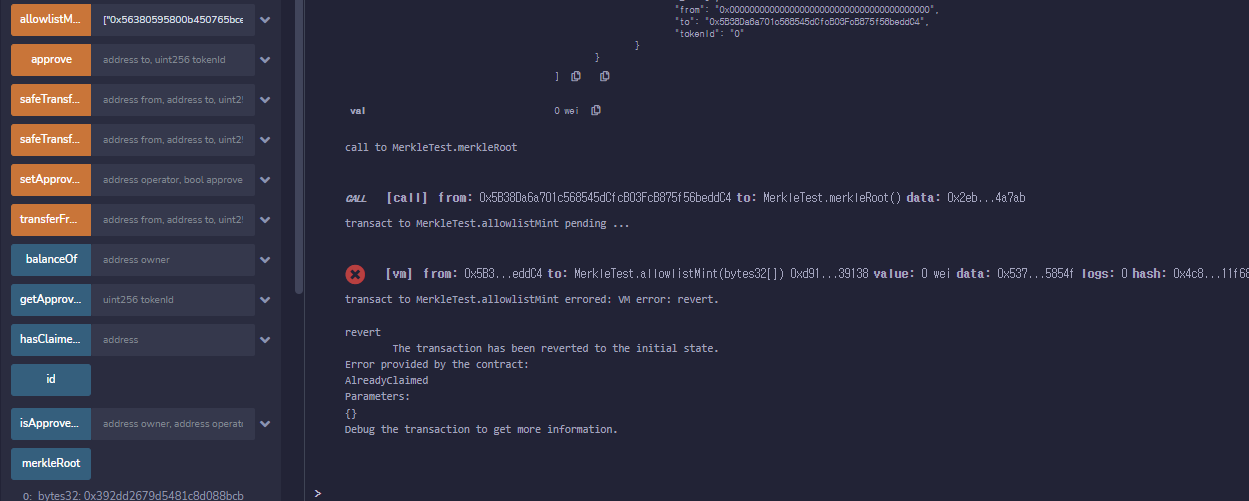
한번 더 같은 함수를 실행해보자. 0x5B38Da6a701c568545dCfcB03FcB875f56beddC4 주소로 이미 민팅을 진행했으므로 AlreadyClaimed 에러가 출력되는 것을 볼 수 있다.
결론
이번 포스팅에서 Merkle Tree와 Merkle Proof에 대해 간략히 설명했으며, 오픈제플린의 Merkle Proof 라이브러리를 살펴보았다. 오픈 제플린의 라이브러리를 통해 높은 보안 수준의 Merkle Proof 구현을 쉽게 사용할 수 있다. 실제로도 암호화 요소를 직접 구현하는 것보다 이렇게 잘 Audit된 라이브러리를 사용하는 것을 권장한다.
많은 NFT 프로젝트가 Merkle Proof를 통해 특정 주소들만 Mint를 수행할 수 있는 기능을 구축하고 있으며, 우리는 온체인에 모든 데이터를 저장할 필요가 없다! 다만, Merkle Tree를 통해 유저들이 Proof를 생성하기 위해선 이 Merkle Tree가 외부에 공개되어야한다. 좀 더 어려운 용어로 말하자면, 우리는 Merkle Proof를 통해 데이터 무결성(Data integrity)를 증명할 수 있지만, Merkle Tree가 공개되어 있지 않다면 Proof 자체를 생성하지 못하므로 데이터 가용성(Data availability) 문제를 해결하지는 못한다. 이를 위해 머클 트리는 IPFS 같은 분산 스토리지와 함께 사용된다.